فصل ششم
توابع خودفراخوان (بازگشتی)
توابع بازگشتی
توابع بازگشتی یکی از روشهای حل مسئله مهم در زبانهای برنامهنویسی است. این مبحث علاوه بر اینکه یک تکنیک برنامهنویسی است، یک راهکار مهم حل مسئله نیز به شمار میآید و میتواند روش جدید تفکر و حل مسئله را نیز به برنامهنویسان و دانشجویان منتقل نماید.
ایده اصلی حل مسئله به شیوه بازگشتی به روش استقرای ریاضی برمیگردد که روشی آشنا برای دانشجویان است. در روش استقرای ریاضی برای اثبات ریاضی مسائل و قضایا به این شیوه عمل میشود که ابتدا برقرار بودن یک رابطه یا قضیه برای حالت پایه مثلاً برای مقدار n = 1 اثبات میشود. سپس با فرض اینکه این رابطه برای مقادیر k و کمتر از آن برقرار باشد، باید ثابت شود که برای مقدار k+1 نیز برقرار است. چنانچه بتوانیم هم حالت پایه و هم حالت استقرایی را اثبات کنیم، میتوانیم نتیجه بگیریم که آن رابطه برای همه مقادیر n برقرار است.
در روش بازگشتی نیز به همین شکل عمل میشود. برای حل یک مسئله ابتدا حالت پایه را در نظر میگیریم و مسئله را برای مقدار پایه حل میکنیم. معمولاً حل مسئله برای مقدار پایه آسان است. در گام بعدی رابطه بازگشتی را برای مسئله موردبحث پیدا میکنیم. بهعنوانمثال فرض کنید میخواهیم مسئله فاکتوریل را بهصورت بازگشتی حل کنیم. اولین گام حل مسئله بهصورت بازگشتی پیدا کردن حالت پایه و رابطه بازگشتی است که در گام بعدی باید این روابط به برنامه تبدیل شود. حالت پایه مسئله فاکتوریل را میتوانیم برای مقدار 0 یا 1 تعریف کنیم:
حال باید رابطه بازگشتی را تعریف کنیم. در تعریف رابطه بازگشتی باید یک مسئله را به حل همان مسئله با اندازه کوچکتر تبدیل کنیم. در این مثال خاص، باید تعریف n! به مسئله ! با اندازه کوچکتری تبدیل شود. به سهولت میتوان به این رابطه به شکل زیر دست پیدا کرد:
همانگونه که مشاهده میشود، محاسبه n! به محاسبه (n-1)! منوط و مربوط شده است. حال کافی است بتوانیم (n-1)! را محاسبه کنیم.
پس از پیدا کردن حالت پایه و رابطه بازگشتی میتوانیم تابع محاسبه فاکتوریل را بهصورت بازگشتی بنویسیم:
جهت روشنتر شدن موضوع به نحوه کارکرد این تابع میپردازیم. برای این منظور از مدل پشته استفاده میکنیم. وقتی تابعی فراخوانی میشود، بازگشتی یا غیر بازگشتی، سیستم کامپیوتر محلهای ذخیره موقتی برای پارامترهای واقعی و متغیرهای محلی (اتوماتیک) ایجاد میکند. این محلهای ذخیره موقتی ناحیهای از حافظه است که پشته زمان - اجرا نامیده میشود. وقتی تابع بازمیگردد، پارامتر و متغیرها محلی آن از پشته زمان ـ اجرا حذف میشوند. هر بار که تابع خودش را فرامیخواند، یک مقدار بیشتری از پشته زمان ـ اجرا برای ذخیره متغیرهای جدید استفاده میشود. اگر هیچگاه زنجیره فراخوانیها به حالت پایه نرسد، در آخر، تمام فضای حافظه برای پشته استفاده میشود. در آن نقطه، برنامه با یک پیام خطا مانند «سرریز پشتة زمان ـ اجرا» متوقف میشود، یا اصطلاحاً کامپیوتر hang میکند. اطلاعاتی که برای یک تابع در پشته ثبت میشود تا زمان پایان فراخوانی آن در پشته باقی میماند.
برای مثال فرض کنید میخواهیم !5 را محاسبه کنیم (شکل 6-1). پس تابع با پارامتر 5 فراخوانی خواهد شد. محاسبه فاکتوریل 5، منجر به فراخوانی تابع فاکتوریل با پارامتر 4 خواهد شد. محاسبه فاکتوریل 4 نیز منجر به فراخوانی تابع فاکتوریل با پارامتر 3 میشود. به همین ترتیب محاسبه !3 منجر به فراخوانی تابع با مقدار 2 میشود. نهایتاً محاسبه فاکتوریل 2 باعث فراخوانی تابع با پارامتر 1 خواهد شد. محاسبه !1 حالت پایه محسوب میشود و جواب آن از قبل مشخص است. عملاً این فراخوانیها تشکیل یک زنجیره فراخوانی تابع میدهند. ازآنجاییکه در این نوع توابع مسئله از طریق فراخوانی خود تابع حل میشود، اصطلاح توابع خودفراخوان برای آن مناسبتر به نظر میرسد. وقتی مقدار حالت پایه مشخص شد، این زنجیره از پایین به بالا جمع خواهد شد. عدد 1 جایگزین فاکتوریل 1 در مستطیل مربوط به محاسبه فاکتوریل 2 میشود و جریان بازگشت فراخوانیها به همین ترتیب ادامه پیدا میکند. در گام آخر عدد 24 جایگزین فاکتوریل 4 شده و فاکتوریل 5 از ضرب آن در 5 به دست میآید و بهعنوان نتیجه نهایی برگردانده میشود.
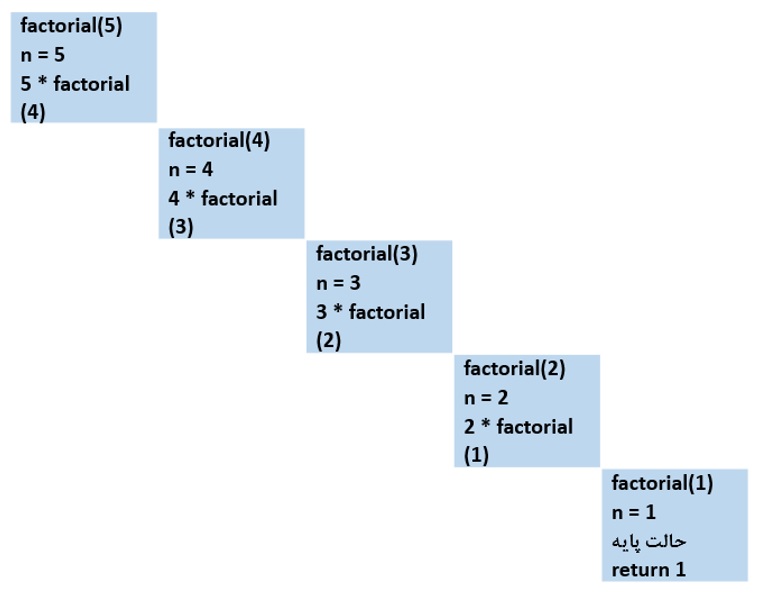
شکل 6-1: نمایی از زنجیره فراخوانی و پشته زمان اجرای تابع بازگشتی فاکتوریل (مقادیری که در پرانتز نوشته شده، مقدار برگشتی فراخوانی مرحله بعدی را نشان میدهد)
روش بازگشتی حل مسئله از چند منظر بسیار حائز اهمیت است. اولاً معمولاً راهحل بازگشتی سادهتر و مختصرتر از راهحل غیر بازگشتی است. ثانیاً بسیاری از مسائل بسیار پیچیده را میتوان به شیوه بازگشتی بهسادگی حل کرد. درواقع کافی است در راهحل بازگشتی رابطه بازگشتی را پیدا کرد. در ادامه طی چند مثال مختلف سعی خواهیم کرد راهحل بازگشتی را با جزئیات بیشتر مرور کنیم.
حل بازگشتی تابع توان
پیشازاین در فصل 3، تابع توان را به کمک حلقه تکرار نوشتیم. اکنون میخواهیم محاسبه توان را بهصورت بازگشتی انجام دهیم. ابتدا باید رابطه بازگشتی توان را پیدا کنیم. با کمی تعمق میتوانیم به این رابطه دستیابیم:
حالت پایه را زمانی در نظر میگیریم که N به 1 رسیده باشد. حال میتوانیم تابع بازگشتی محاسبه توان را بهصورت زیر تعریف کنیم:
به شیوه نوشتن توضیحات در این مثال دقت کنید. علاوه بر توضیحات معمول، سه بخش جدید در این تابع ملاحظه میشود: پیششرطها، پس شرطها و توجه . پیششرطها مجموعه شرایطی هستند که برای استفاده درست از این تابع باید برقرار باشند، بهعنوانمثال فرض شده است که n حتماً مثبت است. پس شرطها، شرایطی هستند که پس از اجرای تابع حتماً برقرار هستند، بهعنوانمثال انتظار میرود مقدار خروجی تابع با xn برابر باشد. توجه، ملاحظاتی را مشخص میکند که در هنگام کار با تابع ممکن است با آن مواجه شویم، بهعنوانمثال یادآوری شده است که در صورت بزرگ بودن n، احتمال بروز خطای سرریز وجود دارد. استفاده از چنین توضیحاتی در ابتدای هر تابعی اعم از ساده یا بازگشتی بسیار مفید خواهد بود.
حل بازگشتی دنباله فیبوناچی
گفته میشود فیبوناچی به مسئله زادوولد خرگوشها با فرضیات زیر پرداخته که منجر به کشف دنبالهای از اعداد با ویژگیهای خاص شده که امروزه به نام او مشهور است. این مسئله به این شکل بیان میشود:
فرض کنید یک جفت خرگوش نر و ماده وجود دارد که همینالان به دنیا آمدهاند. خرگوشها پس از یک ماه بالغ میشوند. فرض میکنیم هر خرگوش ماده بهمحض بلوغ حتماً باردار شود و دوران بارداری نیز یک ماه باشد. همچنین فرض میکنیم در هر بارداری یک خرگوش نر و یک ماده به دنیا بیاید. با فرض اینکه خرگوشها هرگز نمیرند، میخواهیم حساب کنیم که پس از n ماه چند جفت از این خرگوشها خواهیم داشت؟
در نقطه شروع یک جفت خرگوش داریم و پس از گذشت یک ماه، باز هم یک جفت خرگوش خواهیم داشت که خرگوش ماده بعد از یک ماه باردار خواهد شد. طبق فرضیات مسئله در ماه بعد یک جفت خرگوش جدید به دنیا خواهد آمد و تعداد خرگوشها به دو جفت میرسد. در ماه بعد مجدداً یک جفت خرگوش جدید به دنیا میآید و تعداد خرگوشها را به سه جفت میرساند. به همین ترتیب در ماه n ام، تعداد جفت خرگوشها برابر خواهد بود با تعداد جفت خرگوشها در ماه قبل بهعلاوه تعداد خرگوش جدیدی که متولد میشود. با توجه به دوره بلوغ و بارداری این تعداد برابر خواهد بود با تعداد جفت خرگوشها در دو ماه قبل. بنابراین هر جمله این دنباله برابر خواهد بود با مجموع دو جمله قبلی:
در این مثال خاص دو جمله اول دنباله، حالت پایه محسوب میشود. همچنین رابطه بازگشتی بهصورت زیر تعریف میشود:
تابع بازگشتی فیبوناچی بر اساس رابطه بازگشتی فوق، بهصورت زیر تعریف میشود:
نحوه فراخوانی تابع fib برای محاسبه جمله پنجم، در شکل 6-2 نشان داده شده است. همانگونه که مشاهده میشود، محاسبه جمله 5، منجر به محاسبه جمله 3 و 4 میشود. محاسبه جمله 4 خود باعث فراخوانی تابع با مقادیر 3 و 2 خواهد شد و زنجیره فراخوانیها به همین ترتیب ادامه پیدا میکند. همانگونه که در این شکل مشخص است، برای محاسبه جمله 5، دو بار جمله سوم محاسبه میشود. همینطور سه بار جمله دوم محاسبه شده است.

شکل 6-2: دنباله فراخوانی¬های محاسبه دنباله فیبوناچی برای جمله پنج
مسئله بزرگترین مقسومعلیه مشترک
محاسبه بزرگترین مقسومعلیه مشترک (ب.م.م ) دو عدد نیز جزو مثالهای معروف الگوریتمهای بازگشتی است. یکی از روشهای معروف پیدا کردن ب.م.م. الگوریتم اقلیدس یا همان روش نردبانی است که در شکل 6-3 نشان داده شده است. در این روش تقسیم اعداد بهصورت متوالی انجام میشود تا به نقطهای برسد که باقیمانده صفر شود. بهعنوانمثال برای پیدا کردن ب. م. م. 846 و 204 ابتدا این دو عدد را تقسیم کرده، خارجقسمت و باقیمانده را محاسبه میکنیم (به ترتیب 4 و 30). در مرحله بعد تقسیم 204 بر باقیمانده یا همان 30 انجام میشود و مجدداً خارجقسمت و باقیمانده محاسبه میشود. باقیمانده این تقسیم برابر 24 خواهد بود. در مرحله بعد باید تقسیم 30 بر 24 انجام شود و کار به همین ترتیب ادامه پیدا میکند. برای درک رابطه بازگشتی در این مثال کافی است به روش نردبانی دقت کنیم، درواقع مسئله ب. م. م. اعداد 846 و 204 در مرحله اول به مسئله ب. م. م. اعداد 204 و 30 تبدیل شده است. همینطور مسئله پیدا کردن ب. م. م. 204 و 30 به مسئله ب. م. م. 30 و 24 تبدیل میشود و به همین ترتیب کار ادامه پیدا میکند.
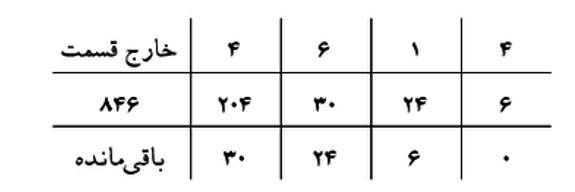
شکل 6-3: پیداکردن بزرگ¬ترین مقسوم علیه مشترک با روش نردبانی
بنابراین رابطه بازگشتی را میتوانیم بهصورت زیر تعریف کنیم:
حالت پایه وقتی است که باقیمانده 0 شود یا به عبارتی عدد دوم 0 باشد. در این صورت عدد اول جواب مسئله است. رابطه بازگشتی نیز، تبدیل ب. م. م. دو عدد به ب. م. م. عدد دوم و باقیمانده آنها است. این رابطه را میتوان در زبان ++C بهصورت زیر تعریف نمود:
حال فرض کنید میخواهیم ب. م. م. 846 و 204 را پیدا کنیم. زنجیره فراخوانی به شکل زیر خواهد بود (شکل 6-4):

شکل 6-4: زنجیره فراخوانی تابع gcd
برج هانوی
علاقهمندان به مباحث مختلف طراحی الگوریتم و همینطور شرکتکنندگان مسابقات برنامهنویسی بهخوبی میدانند که یکی از مهمترین پارامترهای طراحی موفقیتآمیز یک الگوریتم، شیوه صحیح فکر کردن روی مسئله است. حل انواع سؤالات الگوریتمی به ما کمک میکند ذهن خودمان را برای حل مسائل پیچیدهتر آماده کنیم. در همین راستا و بهعنوان یک تمرین ساده، به بررسی یکی از روشهای حل مسئله کلاسیک برج هانوی میپردازیم. مسئله برج هانوی یکی از مسائل جذاب، قدیمی و مشهور است که به یک مسئله کلاسیک در علوم رایانه تبدیل شده است.
در محوطه معبدی در آسیای دور سه میله الماسی قرار داشت که یکی از آنها حاوی تعدادی قرص طلایی بود. کاهنان معبد در تلاش بودند تا قرصهای طلائی را از آن میله به یکی دیگر از میلهها تحت شرایطی انتقال دهند، و باور داشتند که با تمام شدن انتقال قرصها عمر جهان نیز به پایان خواهد رسید! میله اولیه ۶۴ قرص داشت، که بر روی هم بهطور نزولی بر اساس اندازهشان چیده شده بودند. نمونه¬ای از برج هانوی در شکل 6-5 نشان داده شده است.

شکل 6-5: نمونهای از برج هانوی
همانند شکل سه میله داریم. یکی از میلهها میله مبدأ (A)، دیگری میله کمکی (B) و دیگری میله مقصد (C) است. هدف انتقال تمام دیسکها از میله مبدأ به میله مقصد با رعایت شرایط زیر است:
• در هر زمان فقط یک دیسک را میتوان جابجا نمود.
• نباید در هیچ زمانی دیسکی بر روی دیسک با اندازه کوچکتر قرار بگیرد.
روش حل این مسئله با سه حلقه در شکل 6-6 نشان داده شده است:
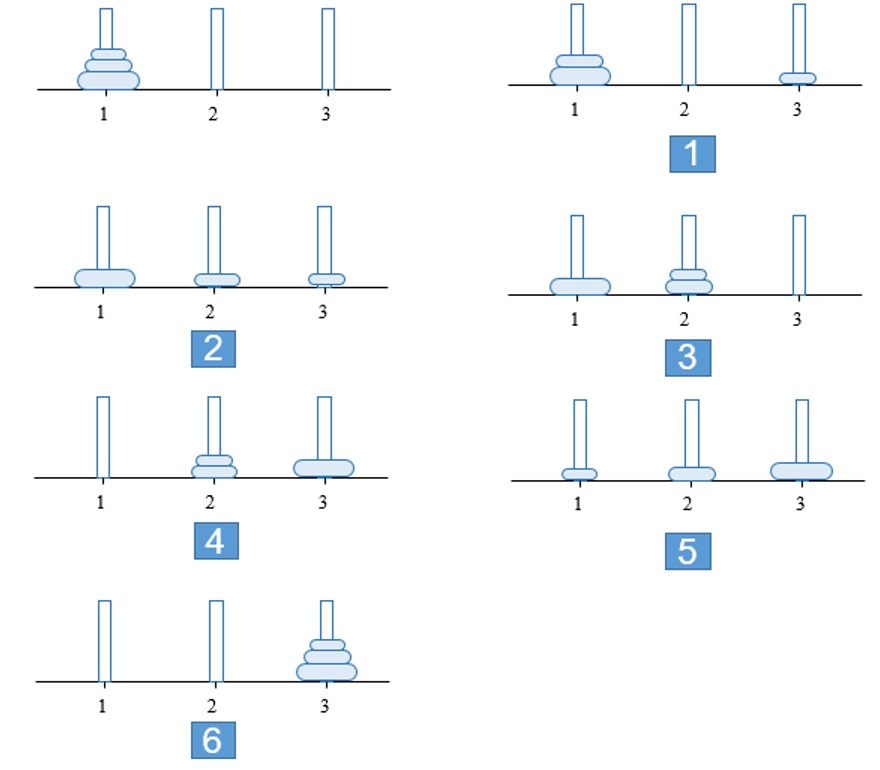
شکل 6-6: حل مسئله برج هانوی با 3 حلقه
برای اینکه مسئلهای بتواند با روش بازگشتی حل شود باید یک ویژگی اساسی داشته باشد. مسئله اصلی (مسئلهای که به ما داده میشود) قابل خرد شدن به زیر مسئلههایی از همان نوع مسئله اصلی باشد، به شرطی که اندازه زیر مسئلههای ایجادشده کمتر باشد. آنگاه میتوان امیدوار بود که آن را بهطور بازگشتی حل کرد! این ویژگی در مورد مسئله برج هانوی صدق میکند. ایده اصلی این است که توجهمان را بهجای حرکت بالاترین دیسک، روی پایینترین دیسک میله متمرکز کرده، و مراحل زیر را طی میکنیم:
• n-1 دیسک بالایی را با شرایط ذکرشده و به کمک میله C به میله B منتقل میکنیم.
• بزرگترین دیسک را از میله مبدأ به میله مقصد حرکت میدهیم.
• n-1 دیسک را که هماکنون در میله B هستند با شرایط داده شده به میله مقصد انتقال میدهیم.
میبینیم که توانستیم عملیات جابجا کردن n دیسک را به دو عملیات مشابه ولی با اندازه کمتر و یک عملیات ساده تقسیم کنیم. واضح است که جابجا کردن n-1 قرص راحتتر از جابجا نمودن n قرص است.
حل بازگشتی برج هانوی به زبان ++C بهصورت زیر است:
برای مثال فراخوانی تابع به شکل ('hanoi(3, ‘A’, ‘B’, ‘C مسئله برج هانوی را با سه دیسک که در میله A قرار دارند و با کمک میله B به میله C منتقل خواهد شد، حل میکند. نتیجه این فراخوانی بهصورت زیر خواهد بود:
برای اینکه به کاهنان کمک کنیم، باید دستور ('hanoi(64, ‘A’, ‘B’, ‘C را اجرا کنیم. ولی چه زمانی طول میکشد تا این دستور اجرا شود؟ در حالت کلی میخواهیم بدانیم اگر تعداد دیسکها n باشد، کمترین تعداد حرکت برای جابجا نمودن دیسکها چقدر است؟
در ابتدا باید بررسی کنیم که آیا تابع بازگشتی فوق کمترین تعداد حرکت را چاپ میکند؟ جواب مثبت است. زیرا واضح است که برای جابجا کردن بزرگترین دیسک از پایین میله A، بقیه دیسکها باید در میله B باشند. فقط در این صورت این دیسک جابجا میشود. در فراخوانیهای بعدی دیسک دوم ازنظر بزرگی جابجا میشود و الیآخر. پس در این فراخوانیها جابجایی بیهودهای صورت نمیگیرد. همچنین توالی حرکتها برای هر n منحصربهفرد است. یعنی برای یک n دو توالی متمایز از جابجاییها وجود ندارد که تعداد جابجایی آنها کمتر یا مساوی این حالت باشد.
حال به مسئله مرتبه اجرایی مسئله میپردازیم: فرض کنیم T(n) تعداد حرکتهای لازم جهت انتقال n دیسک به مقصد باشد. بر اساس توضیحات فوق T(n-1) حرکت برای انتقال n-1 دیسک به میله کمکی، یک حرکت برای انتقال بزرگترین دیسک به میله مقصد، و باز T(n-1) حرکت برای انتقال n-1 دیسک موجود در میله کمکی به میله مقصد نیاز است. پس میتوان نوشت:
با حل این رابطه بازگشتی داریم:
همانطور که مشاهده میکنیم مرتبه اجرایی این الگوریتم 2n است که هرچند مرتبه مناسبی نیست، این روش حداقل تعداد حرکتهای ممکن را میدهد.
اگر فرض کنیم کاهنان با سرعت عمل زیاد توانسته باشند بهصورت شبانهروزی و نسل به نسل در هر دو ثانیه یک قرص را جابجا کنند، برای انتقال تمامی ۶۴ قرص به میله مقصد، در حدود ۱٫۱۶۹ تریلیون (میلیون میلیون) سال زمان لازم دارند!
مسئله جستجوی دودویی
جستجوی یک عدد در یک لیست بهصورت زیر قابل انجام است:
در این حالت تکتک اعضای لیست با مقداری که میخواهیم آن را جستجو کنیم مقایسه میشود و درصورتیکه با یکی از آنها تطبیق پیدا کرد، تابع نتیجه مثبت برمیگرداند. چنانچه لیست اعداد از قبل مرتبشده باشد، میتوان از تکنیکها و الگوریتمهای بهتری استفاده نمود که بهمراتب کارآمدتر هستند. الگوریتم جستجوی دودویی یکی از این روشها است. روش کار این الگوریتم در شکل 6-7 نشان داده شده است.
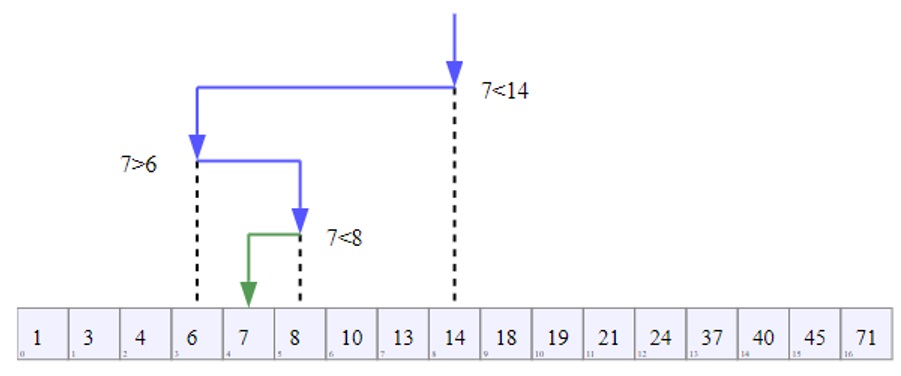
شکل 6-7: جستجوی دودویی
در جستجوی دودویی فرض میکنیم که لیست از قبل مرتبشده است. به عددی که در حال جستجوی آن هستیم اصطلاحاً کلید گفته میشود. فرض کنید در لیستی که در شکل زیر نشان داده شده است، میخواهیم عدد 7 را جستجو کنیم. روش کار به این صورت است که ابتدا وسط لیست را پیدا میکنیم. عنصر وسط لیست را با کلید (عدد 7) مقایسه میکنیم. اگر کلید کوچکتر از عنصر وسط بود، باید نیمه سمت چپ یا نیمه اول لیست را جستجو کنیم و چنانچه کلید بزرگتر از عنصر وسط لیست باشد، باید نیمه دوم لیست جستجو شود. بهعبارتدیگر با یک مقایسه ساده، فضای جستجو را نصف خواهیم کرد. در این مثال 7 کوچکتر از عنصر وسط یا همان 14 است. لذا باید کلید را در بین 8 عدد اول لیست جستجو کنیم. مجدداً عنصر وسط را پیدا میکنیم. در این مرحله عنصر وسط 6 است و کلید بزرگتر از آن خواهد بود. پس باید جستجو در خانههای 4 تا 7 انجام شود. یکبار دیگر عنصر وسط این بخش یعنی خانههای 4 تا 7 را پیدا میکنیم (خانه 5 با مقدار 8). با توجه به اینکه کلید از 8 کوچکتر است، باید جستجو در سمت چپ آن ادامه پیدا کند که تنها شامل یک خانه یا همان خانه 4 است. حال اگر مقدار این خانه برابر 7 باشد، به این معنی است که الگوریتم جستجوی دودویی توانسته است کلید را در خانه 4 پیدا کند. در غیر این صورت کلید در لیست وجود نداشته است. برنامه جستجوی دودویی بهصورت زیر است:
در این برنامه متغیرهای first و last محدوده مورد جستجو را در آرایه مشخص میکنند. هر بار نقطه وسط این محدوده (midpoint) محاسبه میشود و تصمیم گرفته میشود که جستجو در نیمه سمت چپ یا راست آن ادامه پیدا کند.
تابع جستجوی دودویی را بهصورت بازگشتی نیز میتوان تعریف نمود:
در حل بازگشتی، هر بار اندازه لیست نصف شده و تابع جستجو روی نصف قسمت قبل فراخوانی میشود. بهعنوانمثال در مرحله اول با مقایسه عنصر وسط لیست با کلید، تصمیم گرفته میشود که تابع بهصورت بازگشتی روی نیمه چپ یا راست آرایه فراخوانی شود. در هر مرحله محدوده مورد جستجو با پارامترهای start و end تعیین میشود. بسته به اینکه کلید مورد جستجو از عنصر وسط این محدوده که دارای زیرنویس mid است کوچکتر باشد، جستجو در محدوده بین start و mid دنبال میشود و در غیر این صورت در محدوده بین mid و end. همچنین اگر مقدار خانه mid با کلید برابر باشد، تابع با نتیجه مثبت پایان میپذیرد.
حل مسئله ـ مطالعه یک مورد
تبدیل اعداد صحیح دهدهی به اعداد صحیح دودویی (تغییر مبنای شمارش از10) به 2)
مسئله : نمایش اعداد در مبنای 10 موجود است. نمایش آنها را در مبنای 2 میخواهیم.
بحث : الگوریتم این تغییر مبنا چنین است
• عدد دهدهی را گرفته بر 2 تقسیم کنید.
• باقیمانده را رقم سمت راستترین جواب قرار دهید.
• جای مقسوم اصلی، خارجقسمت را قرار دهید.
• تکرار کنید و هر باقیمانده جدیدی را در سمت چپ باقیمانده قبلی قرار دهید.
• وقتی خارجقسمت صفر شد خاتمه دهید.
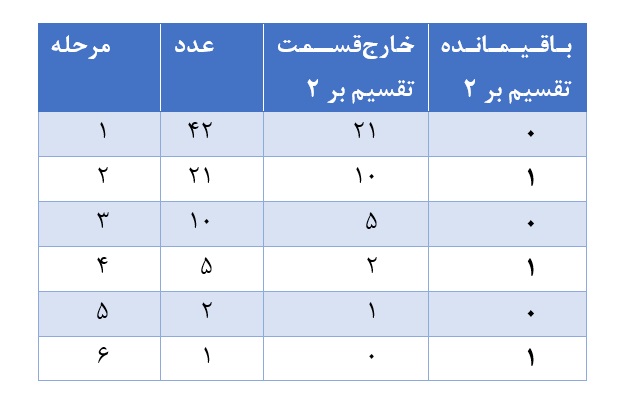
به مثالی توجه کنید تا قبل از نوشتن برنامه، شناخت بیشتری راجع به مسئله پیدا کنید. فرض کنید 42 را بخواهیم از مبنای 10 به مبنای 2 ببریم. به خاطر داشته باشید که خارجقسمت مرحله قبل مقسوم مرحله بعد است.
باقیمانده تقسیم بر 2 خارجقسمت تقسیم بر 2 عدد مرحله
جواب، دنباله باقیماندهها از آخر به اول است. لذا عدد دهدهی 42 در مبنای دودویی 101010 است.
در مثال فوق باید 42 % 2 بعد از(42/2) % 2 چاپ شود. همینطور (42/2) % 2 را باید بعد از ((42/2)/2) % 2 چاپ کنیم. به نظر میرسد که ماهیت برگشتی مسئله در حال ظهور است. یعنی میتوانیم بگوییم که برای هر عدد داده شده مثل number باید number % 2 را بعد از (number/2) % 2 چاپ کنیم. الگوریتم زیر نتیجه بحث فوق است.
پیادهسازی آن در C++ چنین است:
کد فوق را برای تبدیل 10 پی میگیریم. توجه کنید که در مثال اولیه ما در مرحله 3 خارجقسمت 10 بود.
فراخوانی :1 تابع Convert با پارامتر واقعی 10 فراخوانی میشود. چون number برابر صفر نیست عبارت بخش شرط اجرا میشود. اجرا تا کامل شدن فراخوانی بازگشتی Convert با مقدار واقعی (number/2) متوقف میماند.
فراخوانی 2: number اکنون 5 است. چون number برابر صفر نیست، اجرای این فراخوانی تا کامل شدن فراخوانی بازگشتی Convert با مقدار واقعی number/2 متوقف میماند.
فراخوانی 3: number برابر 2 است چون number برابر 0 نیست. اجرا این فراخوانی تا کامل شدن فراخوانی بازگشتی Convert با مقدار واقعی number/2 متوقف میماند.
فراخوانی 4: number برابر 1 است. چون number برابر 0 نیست. اجرا این فراخوانی تا کامل شدن فراخوانی بازگشتی Convert با مقدار واقعی number/2 متوقف میماند.
فراخوانی 5: number برابر 0 است. اجرا این فراخوانی کامل است و کنترل به فراخوانی قبلی برمیگردد.
فراخوانی 4: اجرای این فراخوانی با دستور بعد از فراخوانی بازگشتی ادامه مییابد. مقدار number%2 (1) چاپ میشود. اجرای این فراخوانی کامل میشود.
فراخوانی 3: اجرای این فراخوانی با دستور بعد از فراخوانی بازگشتی ادامه مییابد مقدار number%2 (0) چاپ میشود. اجرای این فراخوانی کامل میشود.
فراخوانی 2: اجرای این فراخوانی با دستور بعد از فراخوانی برگشتی ادامه مییابد. مقدار number%2 (1) چاپ میشود. اجرای این فراخوانی تمام میشود.
فراخوانی 1: اجرای این فراخوانی با دستور بعد از فراخوانی برگشتی ادامه مییابد. مقدار number%2 (0) چاپ میشود. اجرای این فراخوانی تمام میشود چون این فراخوانی بازگشتی نیست اجرای برنامه ادامه پیدا میکند.
روش بازگشتی یا حلقه تکرار؟
همانگونه که احتمالاً تاکنون متوجه شدهاید، روش بازگشتی تا حدی شبیه حلقههای تکرار است و میتواند در برخی مسائل جایگزین روش حل با حلقه تکرار شود. در روش بازگشتی تکرار فرایند با فراخوانی تابعی که خودش را فرامیخواند، انجام میشود. حالت پایه برای خاتمه زنجیره تکرار فراخوانیها مورد استفاده قرار میگیرد.
حال این سؤال مطرح میشود که روش بازگشتی بهتر است یا حلقههای تکرار (حل غیر بازگشتی)؟ جواب سادهای برای پاسخ به این سؤال وجود ندارد. انتخاب معمولاً بستگی به دو موضوع دارد: کارآیی و طبیعت مسئلهای که حل میشود.
کارآیی (سرعت اجرا و استفاده از حافظه) معمولاً در روش غیربازگشتی بهتر از بازگشتی است. هر زمان یک فراخوانی بازگشتی انجام میشود، سیستم باید فضای پشته را برای کلیه متغیرهای (اتوماتیک) محلی و پارامترهای واقعی ایجاد کند. هر فراخوانی تابع موجب صرف زمان میشود. در گذشته، در کامپیوترهای با سرعت کم و ظرفیت حافظه محدود، این برتری محسوس بود اما با کامپیوترهای سریع و مدرن امروزی، کاهش سرعت در الگوریتم بازگشتی اغلب محسوس نیست. بنابراین انتخاب بین روش بازگشتی و غیر بازگشتی بیشتر به طبیعت مسئلهای که حل میشود بستگی دارد.
در الگوریتم¬های سادهای نظیر فاکتوریل و توان که قبلاً در این فصل بحث کردیم، تفاوت چندانی بین دو روش وجود ندارد، ولی برای برخی از مسائل نظیر برج هانوی که راهحل بازگشتی بسیار سادهتری دارند، پیدا کردن راهحل غیر بازگشتی دشوارتر است. درمجموع اثبات میشود که هر مسئلهای که بهصورت بازگشتی قابلحل باشد، راهحل غیر بازگشتی هم دارد، اما ممکن است این راهحل بهمراتب پیچیدهتر و طولانیتر باشد.